- Hochschule Trier
- Campus wählen
- Quicklinks
-
- English
In diesem Projekt lernen wir, wie Modellvorhersagen funktionieren und wie man mit einfachen Mitteln Temperatur- und Klimadaten auswerten und prognostizieren kann. Ein mathematsiches Modell ist die Abbildung eines realen Systems in Form eines Computerprogrammes (Digitaler Zwilling). Ein Prognosemodell ist ein Werkzeug für Vorhersagen wie sich das reale System verhalten wird. KI ist ein Oberbegriff für Algorithmen, die lernen, entscheiden und komplexe Aufgaben lösen - und kann auch Prognosemodelle beinhalten.
Ziele:
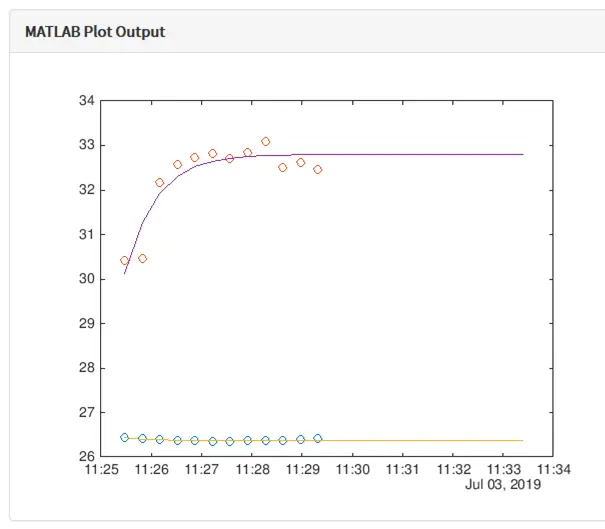
Hier ist ein online Beispiel für eine Temperaturvorhersage im Hörsaal.
Mathematische Prognosemodelle werden genutzt, um zukünftige Entwicklungen vorherzusagen. Man unterscheidet dabei zwischen:
Ein Beispiel für ein White-Box-Modell ist der Spannungsteiler aus der Physik, dessen Spannung U₁ sich auf der Basis physikalischer Gesetze berechnen lässt:
U₁ = R₁ / (R₁ + R₂) * U
Haben wir Informationen über R1, R2 und U, so können wir U1 vorhersagen.
Ein Back-box Modell wäre zum Beispiel die Beschreibung des Temperaturverlaufs T(t) über der Zeit t mit einer linearen Funktion:
T = Steigung * t + Offset
In der Praxis müssen Modelle oft kalibriert werden, da manche Parameter (wie bspw. R₁ oder den Offset) nur ungenau bekannt sind. Mit Hilfe von Messdaten und Optimierungsverfahren kann man solche unbekannten Parameter bestimmen. Das nennt man Modellkalibrierung oder Parameteridentifikation.
Fazit: Bei Prognosemodellen passen wir die Parameter häufig an Messdaten aus der Vergangenheit an, um zukünftige Werte vorhersagen zu können.
Der Unterschied zwischen White-Box- und Black-Box-Modellen wird am Beispiel einer Kuckucksuhr erklärt:
Beide können kurzfristige Vorhersagen treffen. Aber der White-Box-Modellierer kennt auch versteckte Mechanismen – wie z. B. den Kuckuck –, die im Modell berücksichtigt sind. Auf das Klima übertragen:
White-Box-Modelle können potenzielle „Umkipp-Punkte“ (Tipping Points) erkennen – also irreversible, gefährliche Veränderungen, die man mit reinen Black-Box-Modellen möglicherweise nie entdecken würde. Daher sind White-Box-Modelle unverzichtbar für überlebenswichtige Klimavorhersagen.
Klimaprognosen nutzen physikalisch fundierte „White-Box“-Modelle (z. B. Erhaltungssätze, Thermodynamik), um Zielgrößen wie die zukünftige Erdtemperatur abhängig von Einflussgrößen (z. B. CO₂-Emissionen) zu berechnen.
Das Klimasystem ist sehr komplex, da:
Da die Gleichungen schwer umstellbar sind, nutzt man Parameteridentifikation mit historischen Daten zur Kalibrierung. Dennoch bleiben Ungenauigkeiten und Fehlerquellen, weshalb man nur Wahrscheinlichkeitsszenarien angeben kann.
Fazit: White-Box-Klimamodelle sind trotz ihrer Komplexität notwendig, um verlässliche Vorhersagen über zukünftige Entwicklungen zu machen.
Wenn man keine Informationen über innere Zusammenhänge eines Systems besitzt, nutzt man häufig empirische Modelle wie lineare Funktionen oder künstliche neuronale Netze (ANN) – sogenannte „Black-Box“-Modelle. Diese beruhen nur auf vorhandenen Daten, ohne physikalischen Bezug (datengetriebene Modelle).
Ein einfaches Beispiel ist eine lineare Ausgleichsgerade mit den Parametern Steigung und Offset, die aus Messdaten berechnet werden. Solche Modelle können nur kurzfristige Vorhersagen treffen.
Im Praxisbeispiel wird der Temperaturverlauf im Klassenzimmer mit einem linearen Modell geschätzt:
T(t) = Steigung · t + Offset
Mit wenigen Messpunkten kann man diese Parameter berechnen (z. B. mit der Zweipunkteform oder über polyfit in Matlab). Unter der Annahme eines konstanten Verlaufs kann man damit kurzfristige Prognosen machen, z. B. für die nächsten 5 Minuten.
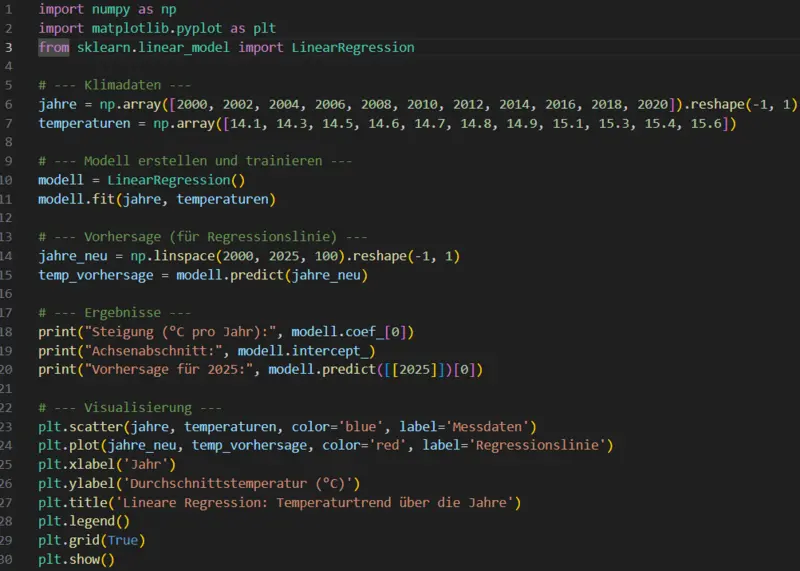
In diesem Abschnitt nutzen wir eine kleine Python-Implementierung, um mithilfe eines einfachen linearen Modells einen Temperaturtrend über die Jahre zu prognostizieren. Unsere Vorgehensweise:
Wir definieren historische Temperaturdaten (z. B. Jahresdurchschnittswerte) und verwenden diese als Trainingsbasis.
Anschließend berechnet das Modell eine Regressionsgerade, also eine Linie der Form
T=a⋅Jahr+b mit a = Steigung (Temperaturanstieg pro Jahr) und b = Achsenabschnitt.Mit dieser Gerade lassen sich zukünftige Temperaturwerte abschätzen (z. B. für ein Jahr in der Zukunft).
Die Visualisierung zeigt sowohl die gemessenen Datenpunkte als auch die Regressionslinie – so wird der Trend unmittelbar sichtbar.
Diese Methode ist bewusst einfach und datenbasiert (also ein Black-Box Ansatz) und eignet sich insbesondere zur anschaulichen Einführung in Prognosemodelle – wie es auf dieser Seite thematisiert wird.
Black-Box-Modell: Lineare Vorhersage mit Zweipunktegleichung einer Geraden
In diesem Beispiel wird ein einfaches lineares Prognosemodell für Temperatur- und Luftfeuchte-Vorhersagen im Klassenzimmer umgesetzt – basierend auf der ThingSpeak-Cloud von MathWorks, mit eigener MATLAB-Integration. Wir verwenden zwei Punkte, um die Steigung und den Offset unserer Vorhersagegeleichung zu ermitteln:
Unsere Gleichung basiert nur auf zwei Punkten Punkt1 zurm Zeitpunkt t1 und Punkt2 zum Zeitpunkt t2. Alle anderen Werte gehen nicht in die Berechnung der Parameter ein. Wollen wir weitere Messungen berücksichtigen, so haben wir mehr Gleichungen (für jenden Messzeitpunkt) als Unbekannte (Offset und Steigung). Dazu nutzen wir in einem späteren Schritt den polyfit-Befehl zur Berechnung einer Ausgleichsgerade (Regressionsgerade).
Schritte zur Umsetzung:
Registrierung bei ThingSpeak
→ Kostenloser Account mit E-Mail-Adresse.
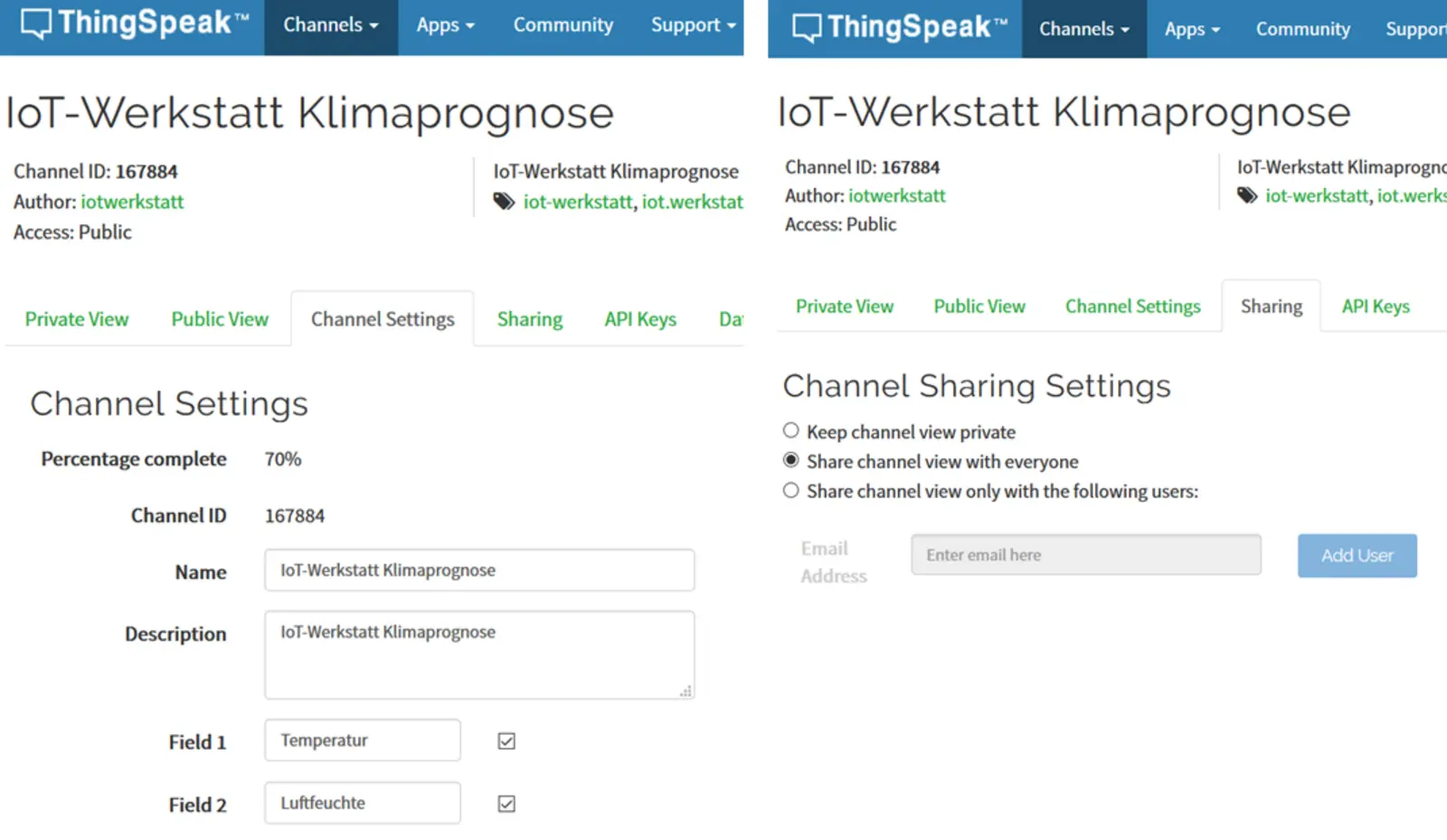
Kanal erstellen
→ Zwei Felder: Temperatur & Luftfeuchte (vgl. unser Kapitel zur Thingspeak-Cloud) .
IoT-Daten senden
→ z. B. via Octopus- oder Makey-Board mit api.thingspeak.com.
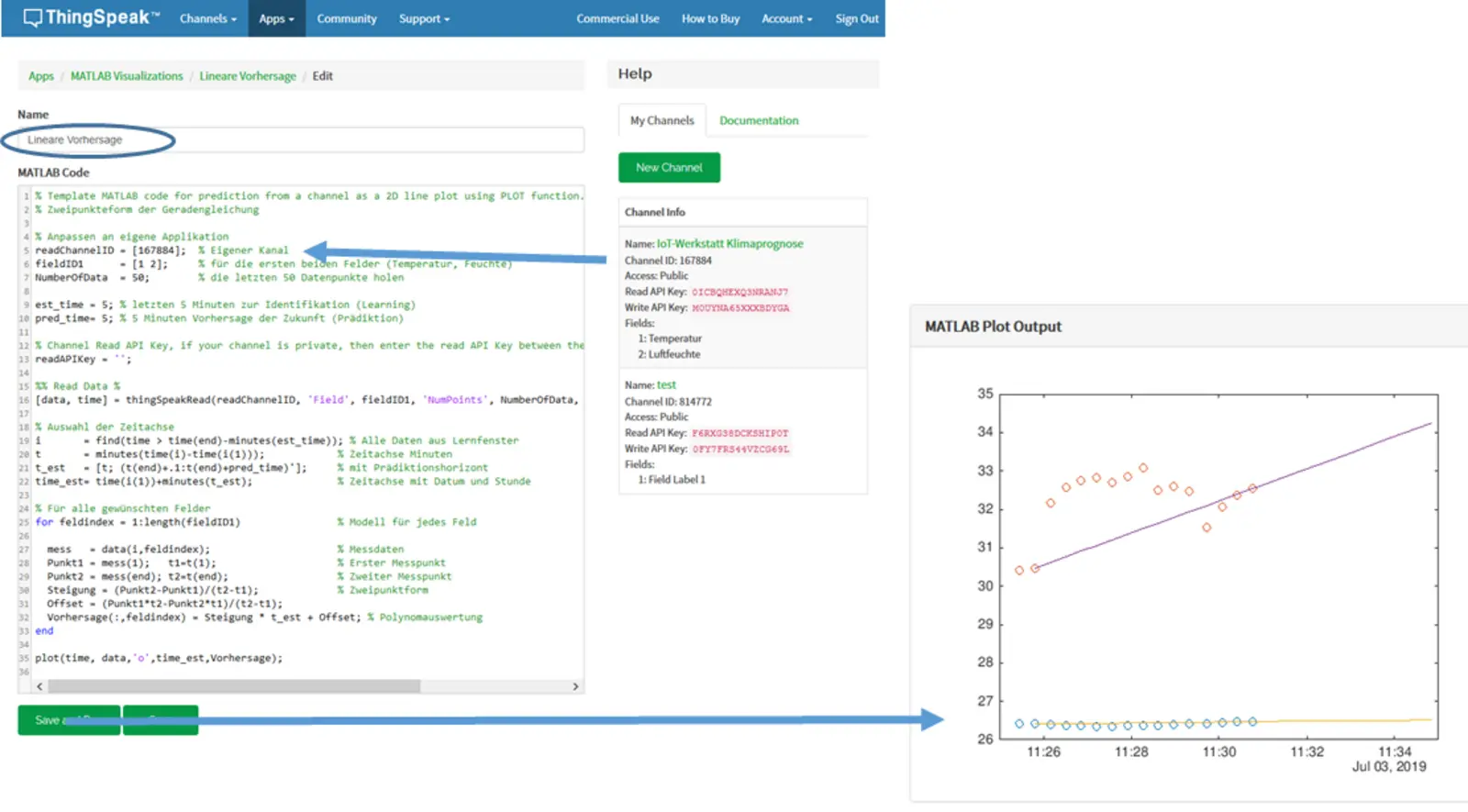
Modell erstellen (Matlab Visualization)
→ ThingSpeak-Daten per MATLAB-Skript auslesen (thingSpeakRead), lineare Funktion berechnen (Steigung & Offset), Prognose für z. B. 5 Minuten simulieren & plotten. Dazu haben wir eine Matlab-Vorlage vorbereitet. Diese mit Cut&Paste in die Matlab-App kopieren und den eigenen Matlab-Kanal dort ergänzen (Channel ID: z.B. 2349799).
Modell testen
→ „Save and Run“ starten, Vorhersage erscheint visuell.
Darstellung einbinden
→ „Add Visualizations“ im ThingSpeak-Dashboard. Hinweis: Aktualisierung nur alle 10 Minuten, manuelles Update nötig für häufigere Prognosen.
Grey-Box-Modell für PT1-Verhalten
Beim Temperaturverlauf im Klassenraum beobachten wir ein sogenanntes PT1-Verhalten (System mit Verzögerung erster Ordnung), z. B. beim Aufdrehen der Heizung oder Öffnen eines Fensters ändert sich die Temperatur exponentiell. Die Temperatur passt sich verzögert an, weil Wände und Luft Wärme speichern.
Mathematisch wird das Verhalten durch die nichtlineare Sprungantwort T(t) = p₁ · (1 – exp(–t / p₂)) beschrieben – mit den Parametern p₁ und p₂, die wir mithilfe eines Grey-Box-Modells bestimmen.
Umsetzung:
Die MATLAB-Vorlage zum Grey-Box-Modell wird hier bereitgestellt.
Live Daten aus dem Hörsaal können hier beobachtet werden.
Sie verlassen die offizielle Website der Hochschule Trier